Clermont Ferrand France Map

Understanding the Power of K-Map Readers: A Comprehensive Guide

Related Articles: Understanding the Power of K-Map Readers: A Comprehensive Guide

Introduction

With great pleasure, we will explore the intriguing topic related to Understanding the Power of K-Map Readers: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.

Understanding the Power of K-Map Readers: A Comprehensive Guide

The realm of data analysis and information retrieval is constantly evolving, with new tools and techniques emerging to address the ever-increasing volume and complexity of data. Among these advancements, K-Map readers have emerged as a powerful tool for navigating and extracting meaningful insights from data, particularly in the domain of Boolean logic and digital circuit design.

This article provides a comprehensive exploration of K-Map readers, their applications, and their significance in modern data analysis. It aims to demystify this tool, elucidating its functionality, benefits, and potential limitations.

What are K-Map Readers?

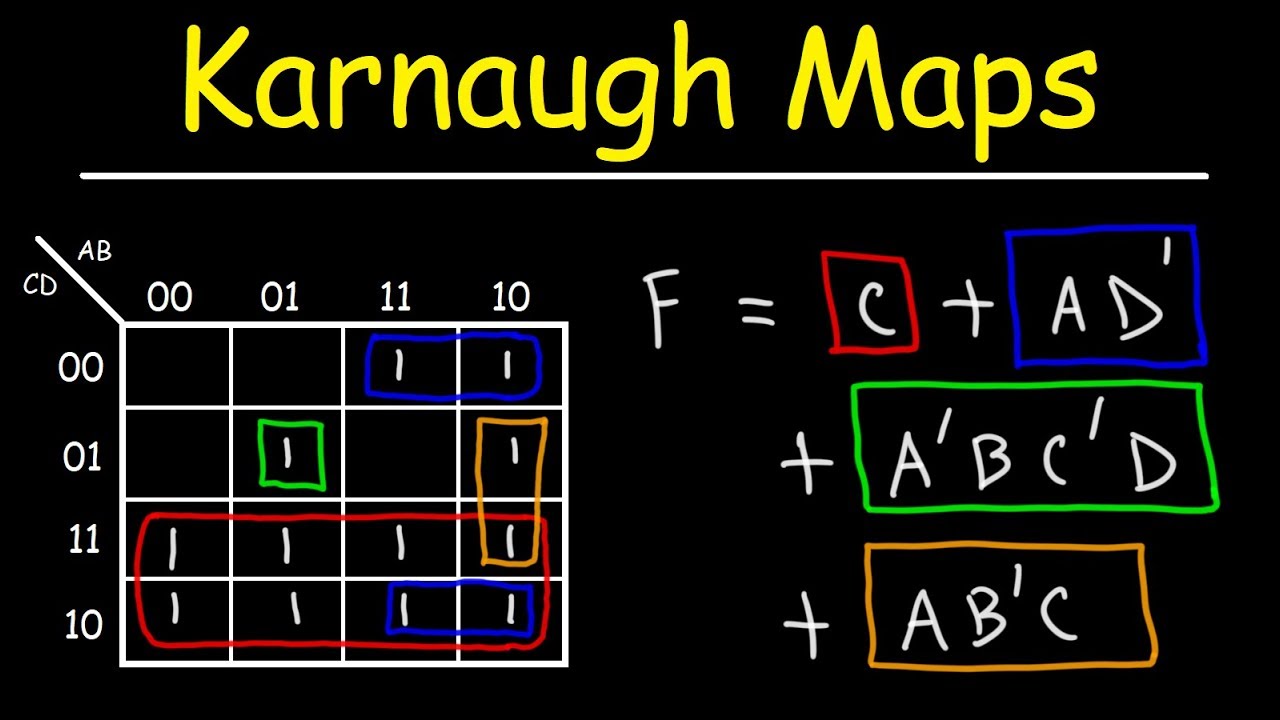
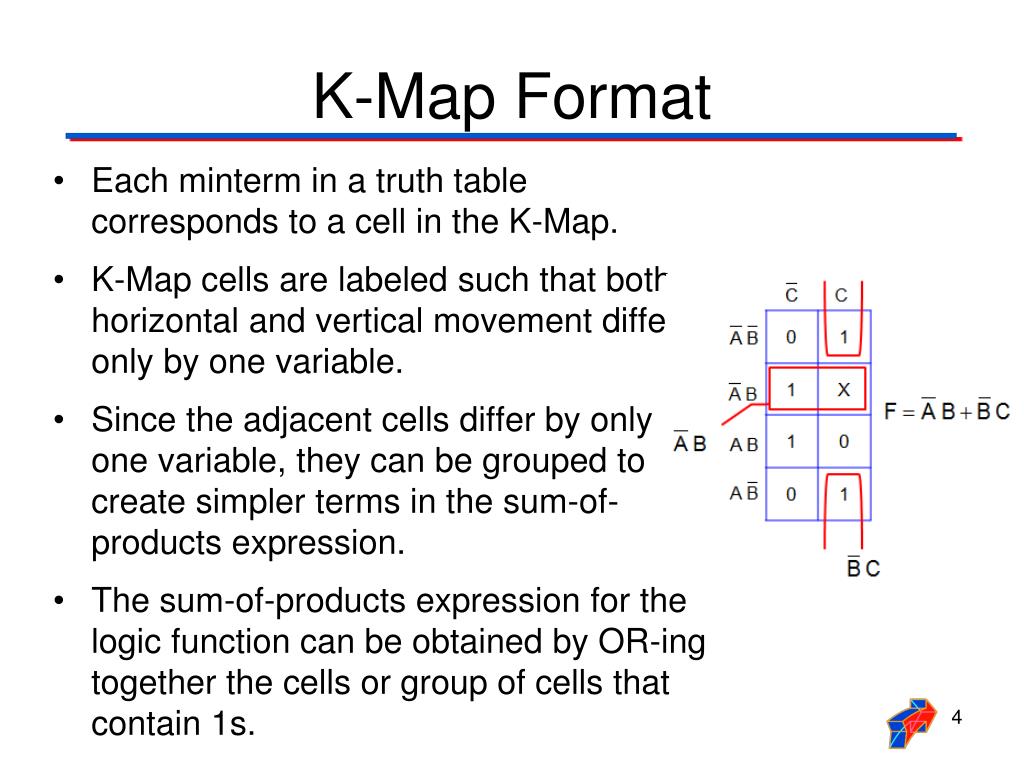
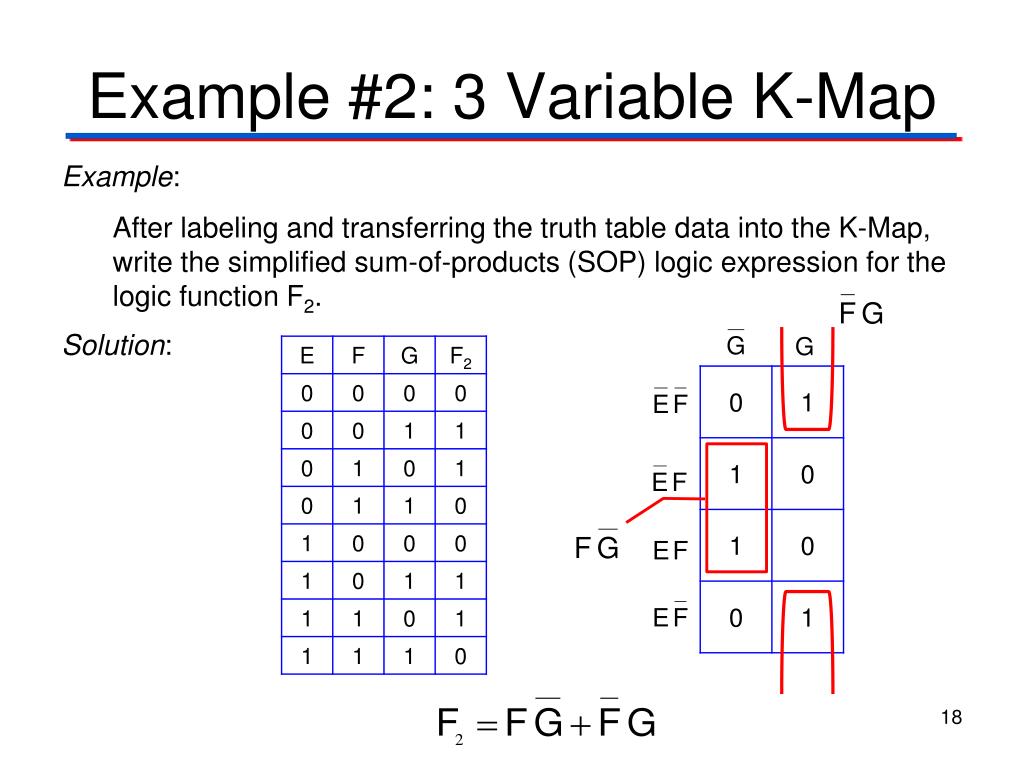
K-Map readers, also known as Karnaugh maps or simply K-maps, are visual representations of Boolean expressions, facilitating the simplification of logical functions and the design of digital circuits. They are essentially graphical tools that utilize a specific arrangement of cells, each representing a unique combination of input variables.

The Core Concept: Simplifying Boolean Expressions

At their heart, K-Map readers excel at simplifying Boolean expressions, which are mathematical expressions that represent logical operations. These expressions often become complex, making it challenging to understand and implement them efficiently. K-Maps provide a visual approach to simplify these expressions, reducing the number of logic gates required in a digital circuit, thereby enhancing efficiency and minimizing cost.

How K-Maps Work: A Step-by-Step Breakdown

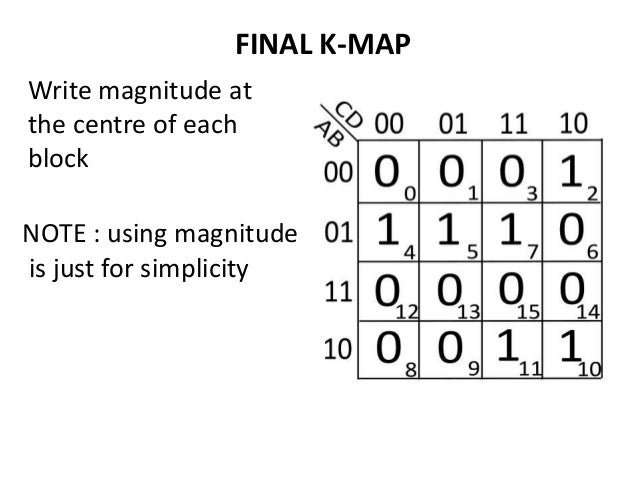
1. Variable Representation: K-Maps are constructed with cells representing all possible combinations of input variables. The number of cells is determined by the number of input variables. For example, a 2-variable K-Map has 4 cells, a 3-variable K-Map has 8 cells, and so on.

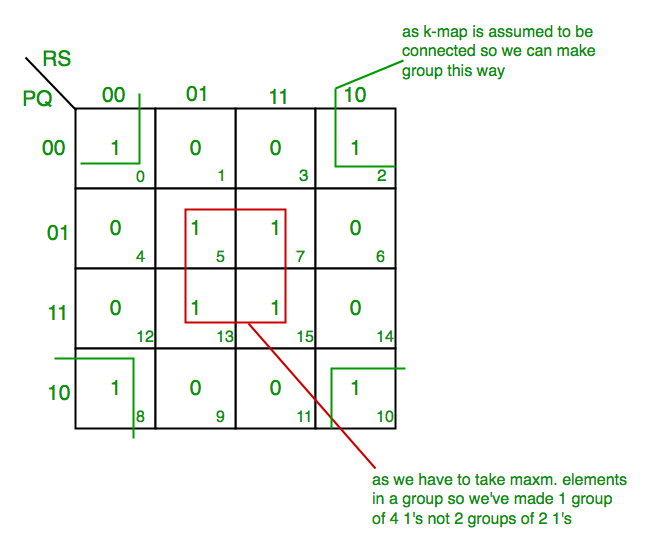
2. Adjacency and Grouping: The key to simplifying Boolean expressions lies in identifying adjacent cells containing "1"s. These adjacent cells represent minterms (product terms) that can be combined. The grouping of adjacent cells follows specific rules, ensuring that each group represents a simplified term.

3. Simplifying the Expression: By grouping adjacent "1"s, the K-Map reader effectively combines minterms, reducing the overall complexity of the Boolean expression. The simplified expression directly translates into a more efficient digital circuit design.

Applications of K-Map Readers:

The applications of K-Map readers extend beyond simplifying Boolean expressions. They are widely used in various fields, including:

• Digital Circuit Design: K-Maps are fundamental tools for designing and optimizing digital circuits. They help in minimizing the number of logic gates required, leading to more efficient and cost-effective circuits.
• Logic Minimization: In computer science, K-Maps are instrumental in minimizing logic functions, reducing the computational complexity of algorithms and improving their efficiency.
• Error Detection and Correction: K-Maps are employed in designing error detection and correction codes, crucial for ensuring data integrity and reliability in communication systems.
• Combinational Circuit Design: They are used for designing combinational circuits, which produce outputs based solely on the current inputs. Examples include adders, decoders, and multiplexers.
• Sequential Circuit Design: K-Maps are also used in the design of sequential circuits, which store previous inputs and use them to determine the current output. This includes flip-flops and counters.

Advantages of Using K-Map Readers:

K-Map readers offer several advantages over traditional algebraic methods for simplifying Boolean expressions:

• Visual Clarity: K-Maps provide a clear visual representation of the Boolean expression, making it easier to identify patterns and simplify the function.
• Efficiency: They significantly simplify the process of Boolean expression simplification, reducing the time and effort required.
• Systematic Approach: K-Maps offer a systematic and structured approach to simplification, ensuring a consistent and reliable outcome.
• Error Reduction: The visual nature of K-Maps helps in minimizing errors that can occur during algebraic simplification.
• Improved Design: K-Map readers lead to more efficient and cost-effective digital circuit designs.

Limitations of K-Map Readers:

While K-Maps are powerful tools, they also have certain limitations:

• Limited to a Few Variables: K-Maps become increasingly complex and cumbersome as the number of input variables increases. Beyond 5-6 variables, they become impractical.
• Not Suitable for Complex Expressions: For highly complex Boolean expressions, K-Maps may not be the most efficient method.
• Limited Functionality: K-Maps primarily focus on simplifying Boolean expressions and may not be suitable for other logic-related tasks.

FAQs about K-Map Readers:

1. What is the maximum number of variables a K-Map can handle effectively?

While theoretically possible, K-Maps become increasingly complex and difficult to use beyond 5-6 variables. For larger numbers of variables, alternative methods like Quine-McCluskey algorithm are more suitable.

2. Can K-Maps be used for both SOP (Sum of Products) and POS (Product of Sums) forms?

Yes, K-Maps can be used for both SOP and POS forms. For SOP, "1"s represent the minterms, and for POS, "0"s represent the maxterms.

3. How do I determine the number of cells in a K-Map?

The number of cells in a K-Map is determined by the number of input variables (n) using the formula 2^n. For example, a 3-variable K-Map will have 2^3 = 8 cells.

4. What are the rules for grouping adjacent cells in a K-Map?

Adjacent cells in a K-Map must differ in only one variable. Groups can be horizontal, vertical, or diagonal, and they must be rectangular or square.

5. Are there any software tools available for creating and using K-Maps?

Yes, several software tools are available, both free and paid, that can help create and analyze K-Maps. Some popular options include Logicly, Logisim, and Multisim.

Tips for Using K-Map Readers Effectively:

• Start with a Clear Understanding of Boolean Logic: Familiarity with Boolean operations and their representation is essential for effectively using K-Maps.
• Choose the Appropriate K-Map Size: Select the K-Map with the correct number of cells based on the number of input variables.
• Identify and Group Adjacent Cells: Carefully identify and group adjacent cells containing "1"s or "0"s, following the rules of adjacency.
• Prioritize Larger Groups: When multiple groupings are possible, prioritize larger groups as they lead to more significant simplification.
• Validate the Simplified Expression: After simplifying the expression, verify its accuracy by comparing it to the original expression.

Conclusion:

K-Map readers are invaluable tools for simplifying Boolean expressions and designing digital circuits. Their visual nature, efficiency, and systematic approach make them a preferred method for logic minimization and circuit optimization. While they have limitations in handling a large number of variables, they remain essential for a wide range of applications in digital design, computer science, and related fields. By understanding their functionality and benefits, users can leverage K-Maps to effectively analyze and manipulate Boolean expressions, leading to more efficient and reliable designs.

Closure

Thus, we hope this article has provided valuable insights into Understanding the Power of K-Map Readers: A Comprehensive Guide. We appreciate your attention to our article. See you in our next article!